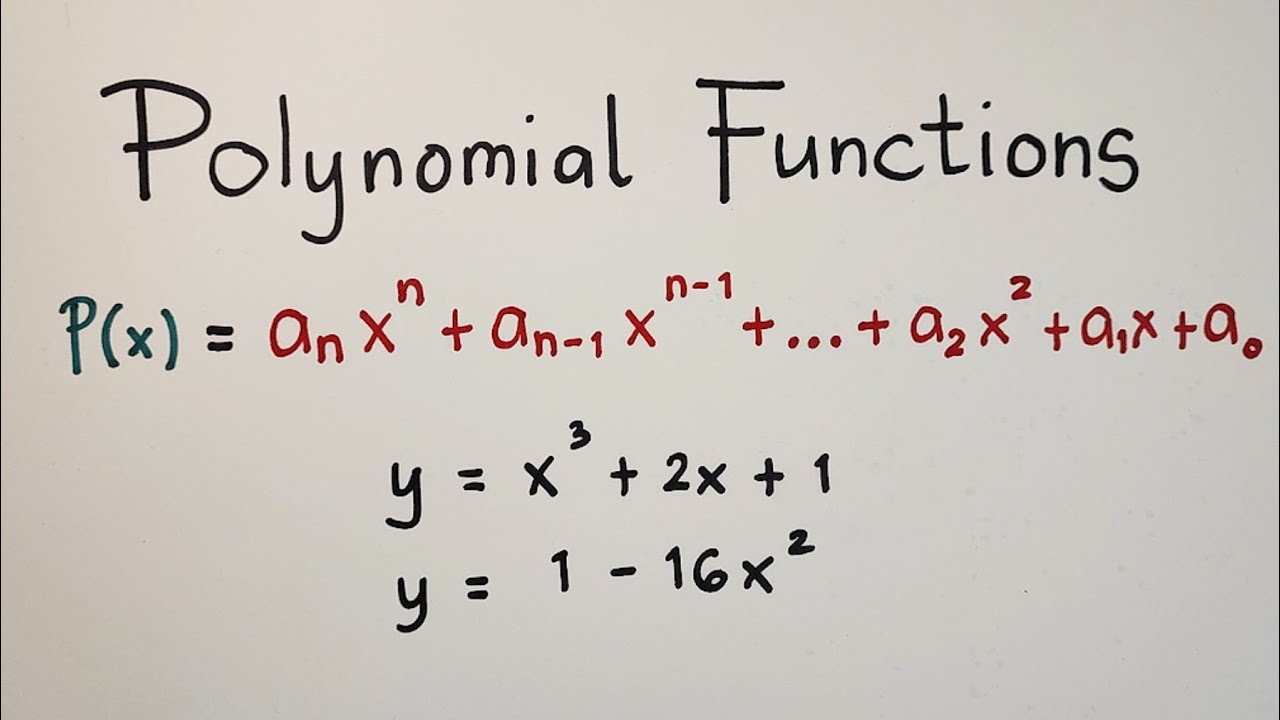Unveiling The Magic Of Polynomial: A Deep Dive Into Its Power And Applications

Polynomial is like the unsung hero of mathematics that quietly shapes the world around us. Whether you realize it or not, polynomials are everywhere – from the algorithms running your favorite apps to the equations governing the physics of our universe. They might sound intimidating at first, but once you peel back the layers, they’re surprisingly approachable and fascinating. Think of them as the building blocks of math, capable of solving some of life’s most complex problems.

Now, I know what you're thinking – math can be a bit dry, right? But trust me, when we break down polynomial into bite-sized chunks, it becomes way more digestible. Imagine a tool that can predict trends, model real-world scenarios, and even help design the next big tech innovation. That’s exactly what polynomial brings to the table. It’s not just numbers; it’s a language that speaks directly to the heart of problem-solving.

So, buckle up because this journey through polynomial isn’t just about equations and graphs. It’s about understanding how something as fundamental as polynomial can shape the future of technology, economics, and even everyday life. Let’s dive in, shall we?

• Stephen Dorff Wife The Story Behind The Spotlight

What Exactly is Polynomial?

Before we get too far ahead of ourselves, let's define what polynomial actually means. At its core, a polynomial is an expression made up of variables, coefficients, and constants combined using addition, subtraction, multiplication, and non-negative integer exponents. Sounds fancy, but it’s really just a mathematical sentence that follows specific rules.

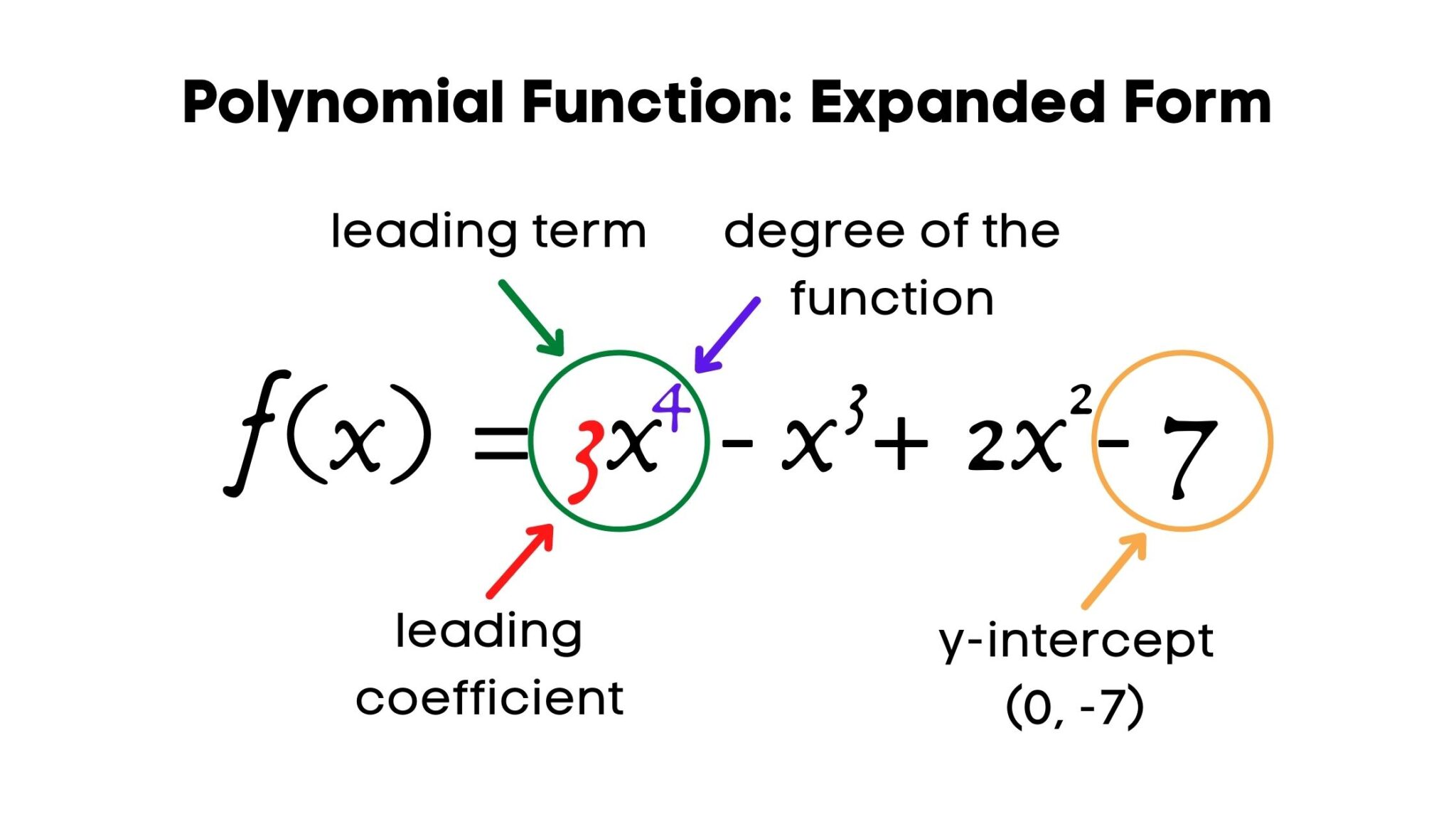
For example, take a look at this simple polynomial: \(3x^2 + 2x - 5\). Here, \(3x^2\) is the leading term, \(2x\) is the middle term, and \(-5\) is the constant. Each piece plays a role in creating the overall expression. Polynomials come in different degrees depending on the highest power of the variable, which we’ll explore in just a bit.

Why Polynomial Matters in Real Life

Now, you might be wondering why polynomial matters outside the classroom. Well, here’s the thing: polynomial isn’t just confined to textbooks. It’s used in everything from engineering and physics to economics and computer science. Let’s break it down with some real-world examples:

• Watch Online Movie Your Ultimate Guide To Streaming Movies Like A Pro

• Engineering: Engineers use polynomials to design structures like bridges and buildings. By modeling forces and stresses, they ensure these constructions are safe and stable.
• Physics: Polynomials help describe motion, energy, and other physical phenomena. For instance, quadratic equations (a type of polynomial) are used to calculate projectile motion.
• Computer Science: Algorithms often rely on polynomial equations to optimize performance, especially in machine learning and data analysis.
• Economics: Economists use polynomial models to predict market trends, analyze consumer behavior, and forecast economic growth.

Types of Polynomial and Their Degrees

Polynomials aren’t all created equal – they come in various forms based on their degree. The degree of a polynomial is determined by the highest power of the variable in the expression. Here’s a quick rundown:

Zero Degree Polynomial

Also known as constant polynomials, these have no variable and only consist of a constant term. For example, \(7\) or \(-4\). They might seem simple, but they form the foundation for more complex equations.

First Degree Polynomial

These are linear polynomials where the highest power of the variable is one. An example would be \(2x + 3\). Linear polynomials are incredibly useful in graphing straight lines and solving basic equations.

Second Degree Polynomial

Quadratic polynomials are second-degree polynomials, and they take the form \(ax^2 + bx + c\). These are widely used in physics and engineering to model parabolic shapes, such as the trajectory of a ball in motion.

How to Solve Polynomial Equations

Solving polynomial equations might sound daunting, but with the right approach, it’s totally doable. Here’s a step-by-step guide:

1. Identify the degree of the polynomial to determine the number of solutions.
2. Set the equation equal to zero if it isn’t already.
3. Factorize the polynomial if possible. This involves breaking it down into simpler expressions that multiply together to give the original polynomial.
4. Use techniques like the quadratic formula for second-degree polynomials or synthetic division for higher degrees.
5. Verify your solutions by substituting them back into the original equation.

For example, solving \(x^2 - 5x + 6 = 0\) involves factoring it into \((x - 2)(x - 3) = 0\), giving solutions \(x = 2\) and \(x = 3\).

Applications of Polynomial in Technology

In the digital age, polynomial plays a crucial role in shaping technology. From optimizing algorithms to creating realistic graphics, its applications are endless. Let’s dive into a few key areas:

Data Compression

Polynomials are used in data compression algorithms to reduce file sizes without losing important information. This is particularly useful in streaming services and cloud storage solutions.

Machine Learning

In machine learning, polynomial regression helps model relationships between variables. By fitting a polynomial curve to data points, algorithms can make accurate predictions and identify patterns.

Cryptography

Polynomials also find their way into cryptography, where they’re used to secure data transmissions. Complex polynomial equations ensure that only authorized parties can access sensitive information.

Polynomial in Nature and Science

Believe it or not, polynomial isn’t just a human invention – it’s deeply embedded in the natural world. From the growth patterns of plants to the orbits of planets, polynomial equations help explain the beauty and complexity of nature.

Growth Models

Scientists use polynomial functions to model population growth, resource consumption, and ecological dynamics. These models help predict future trends and guide conservation efforts.

Physics and Astronomy

In physics, polynomial equations describe everything from the motion of particles to the expansion of the universe. Astronomers rely on these equations to calculate the positions of celestial bodies and study cosmic phenomena.

Challenges and Misconceptions About Polynomial

While polynomial is incredibly powerful, it’s not without its challenges. One common misconception is that higher-degree polynomials always provide better results. In reality, overly complex models can lead to overfitting, where the model fits the data too closely and loses its predictive power.

Another challenge lies in solving higher-degree polynomial equations, which can be computationally intensive. Numerical methods and approximations often come into play to overcome these limitations.

Polynomial in Education: Bridging the Gap

Teaching polynomial can be tricky, especially for students who find math intimidating. However, by breaking it down into relatable concepts and real-world applications, educators can make it more accessible. Interactive tools, visual aids, and hands-on activities can go a long way in helping students grasp the fundamentals.

Interactive Learning Tools

Platforms like Desmos and GeoGebra offer interactive graphing tools that allow students to experiment with polynomial functions. By visualizing how changes in coefficients affect the graph, students gain a deeper understanding of the material.

Future Trends in Polynomial Research

As technology advances, so does the role of polynomial in research and innovation. Researchers are exploring new ways to apply polynomial in fields like quantum computing, artificial intelligence, and renewable energy. These developments promise to unlock even more possibilities in the years to come.

Quantum Computing

Polynomial equations are at the heart of quantum algorithms, enabling faster computations and solving problems previously thought unsolvable. As quantum computers become more mainstream, the demand for polynomial expertise will only grow.

Conclusion: Embracing the Power of Polynomial

In conclusion, polynomial is far more than just a mathematical concept – it’s a tool that shapes our world in countless ways. From engineering marvels to technological breakthroughs, its applications are vast and varied. Understanding polynomial opens doors to solving complex problems and driving innovation.

So, whether you’re a student, a professional, or simply someone curious about the world of math, take the time to explore polynomial. It might just change the way you see the world. And hey, don’t forget to share your thoughts in the comments below or check out our other articles for more insights!

Table of Contents

• What Exactly is Polynomial?
• Why Polynomial Matters in Real Life
• Types of Polynomial and Their Degrees
• How to Solve Polynomial Equations
• Applications of Polynomial in Technology
• Polynomial in Nature and Science
• Challenges and Misconceptions About Polynomial
• Polynomial in Education: Bridging the Gap
• Future Trends in Polynomial Research
• Conclusion: Embracing the Power of Polynomial